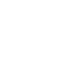
2 - Caractéristiques globales des séries statistiques
Il s’agit de caractériser la série statistique dans sa globalité suivant différents critères. On trouve des caractéristiques de tendances globales (mode, médiane, moyenne) et des caractéristiques de dispersion de la population (étendue de variation, écart type, etc …)
Caractéristiques globales
Le Mode
Le Mode est la valeur de la variable statistique rencontrée le plus fréquemment dans la série statistique. Dans l’exemple précédent le l’analyse statistique de la taille des français, c’est la classe 9 (1m70 à 1m75) qui recueille l’effectif le plus large (124).
Attention : certaines séries statistiques peuvent avoir plusieurs modes. On parle alors de série multimodale.
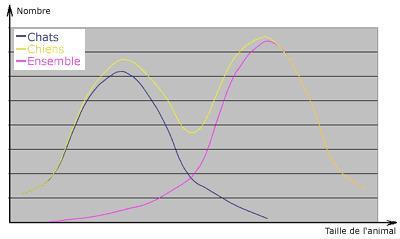
Par exemple, si l’on fait une statistique sur la taille des chats, puis sur la taille des chiens, on obtient des séries à un seul mode. A l’inverse, si l’on regroupe les deux populations pour avoir une statistique sur la taille des animaux de compagnie, on obtient une série à deux modes comme le montre le schéma ci-dessous.
La moyenne arithmétique
La moyenne arithmétique d’une série statistique s’obtient en divisant la somme des valeurs observées par le nombre de valeurs.
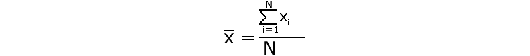
Dans l’exemple précédent, la valeur moyenne (ici la taille moyenne) est obtenue en additionnant les tailles centrales des différentes classes : 1,325 + 1,375 + 1,425 + 1,475 + … + 2,075 + 2,125 et en divisant le résultat par 17 le nombre de classes.
On obtient une taille moyenne de 1,725 c’est à dire le milieu de la classe 9 (1,70 à 1,75.
La moyenne arithmétique pondérée
La moyenne arithmétique précédente (dite « simple ») ne tient pas compte le la répartition de la population en fonction de la valeur de la variable. Elle se situe simplement au milieu de l’intervalle de variation de la variable.
La moyenne arithmétique pondérée tient compte de l’effectif associé à chaque valeur en pondérant cette valeur par cet effectif. Ainsi la moyenne pondérée est égale à la somme des produits de chaque valeur par l’effectif associé divisée par le nombre de valeur selon la formule suivante :
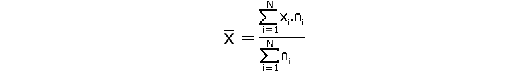
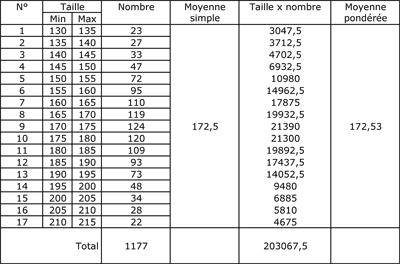
Le calcul de la moyenne pondérée est illustrée par le tableau suivant qui reprend l’exemple de la taille des Français :
La Médiane
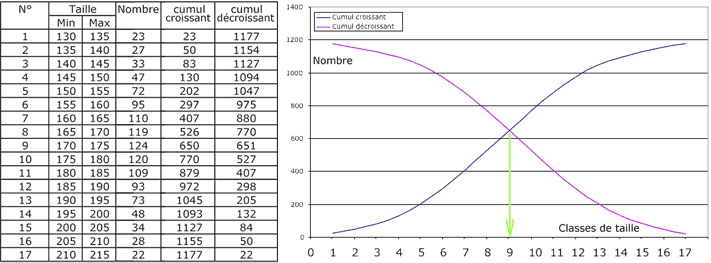
La médiane d’une série statistique est la valeur de la variable pour laquelle les effectifs associés respectivement aux valeurs supérieures et inférieures sont égaux.
On peut déterminer graphiquement la valeur de la médiane en traçant les courbes des cumuls des effectifs respectivement en valeurs croissante et décroissante comme le montre le tableau et le graphique suivant :