3 - Loi normale ou loi de Laplace-Gauss
Présentation
La loi normale a été proposée par Pierre-Simon Laplace (1749-1827) dans son ouvrage : Théorie analytique des probabilités.
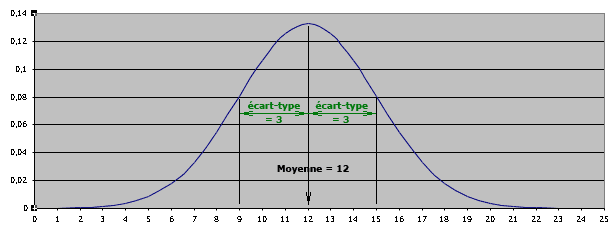
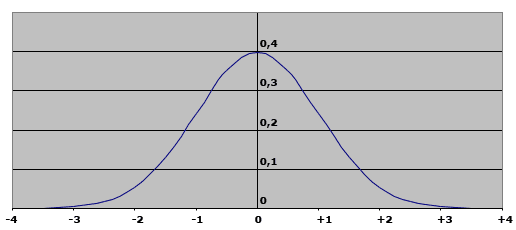
Cette loi caractérise des grandeurs qui se répartissent autour d’une valeur moyenne avec des probabilités qui diminuent de manière symétrique à mesure que l’on s’éloigne de la moyenne. C’est donc une courbe en forme de « cloche » comme celle de la répartition de la taille des Français.
La loi normale se caractérise essentiellement par la moyenne et l’écart-type de la distribution. Elle se formule mathématiquement assez simplement à partir de ces deux paramètres :
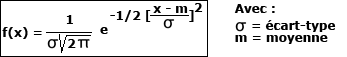
L’allure de la courbe représentant la loi normale est la suivante :
Loi normale centrée réduite
Pour « centrer » la courbe précédente, et la normer par rapport à l’écart-type, il suffit d’effectuer le changement de variable suivant qui fixe l’origine des abscisses au droit de la moyenne :
T = (X – moyenne) /écart-type
On obtient alors la loi normale centrée réduite. On démontre que si une variable aléatoire X suit une loi normale N (m ; sigma) alors la variable aléatoire T = (X – m)/ sigma suit la loi normale centrée réduite : N (0 ;1).
L’équation de la loi normée réduite devient la suivante :
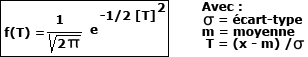
L’allure de la courbe normée est la suivante :
Cette loi normée sera d’une utilisation beaucoup plus facile et on trouvera des tables qui permettent d’évaluer facilement les probabilités associées à certains valeurs ou plage de valeurs de la variable.
On utilisera d’ailleurs plus facilement la fonction de répartition qui calcule la probabilité qu’une variable ait une valeur inférieure à une valeur donnée.
On a superposé ci-dessous, les courbes de la fonction de répartition et de la loi normale réduite centrée :
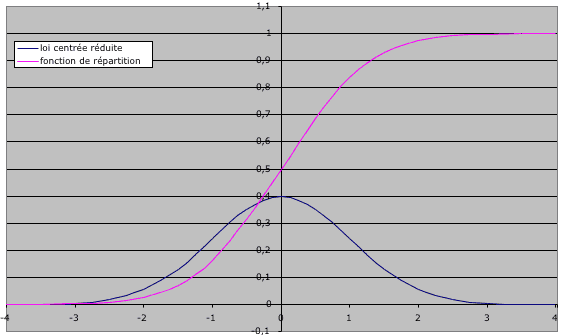
On note que la courbe de la fonction de répartition coupe l’axe des ordonnées avec la valeur 0,5. La probabilité que la variable ait une valeur inférieure à la moyenne est donc de 50 % ce qui confirme la symétrie de la loi normale par rapport à la moyenne.
