3 - Taille d'un échantillon
La taille de l’échantillon a une influence fondamentale sur la précision des estimations réalisées sur les caractéristiques de la population-mère.
Pour des raisons économiques, il est nécessaire d’utiliser une taille d’échantillon la plus réduite possible tout en obtenant un taux de confiance suffisant.
3 paramètres doivent être pris en compte pour la détermination d’une taille minimum d’échantillon :
- La marge d’erreur que l’on se donne pour la grandeur que l’on veut estimer,
- Le taux de confiance que l’on souhaite garantir sur la mesure,
- La proportion connue ou supposée dans la population-mère.
Dans les formules suivantes on appelle :
N : la taille de la population-mère,
n : la taille de l’échantillon,
e : la marge d’erreur,
t : le coefficient de marge déduit du taux de confiance,
p : la proportion des éléments de la population-mère qui présentent une propriété donnée.
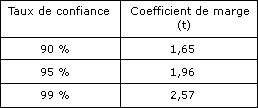
Les taux de confiance les plus utilisés et les coefficients de marge associés sont donnés dans le tableau suivant :
Cas de l’échantillon indépendant (non exhaustif)
La formule donnant la taille de l’échantillon minimum est la suivante :
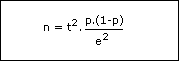
Cas de l’échantillon exhaustif
La formule devient la suivante :
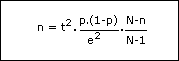
L’application des formules précédentes suppose la connaissance de la proportion d’éléments de la population-mère sur lesquel porte l’étude. deux approches sont possibles :
- Réaliser un pré-sondage sur un échantillon de petite taille pour avoir une approximation de cette proportion,
- Estimer au mieux cette proportion. Dans les formules précédentes, la proportion p est présente sous la forme de la fonction p.(1-p) dont on a représenté ci-dessous la variation :
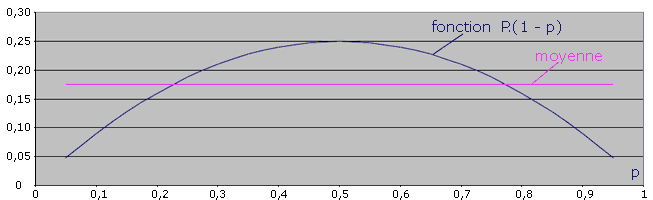
Le terme p.(1-p) varie entre les valeurs 0 et 0,25, avec une moyenne de 0,175. Si l’on veut avoir un majorant de la taille de l’échantillon, on prend la valeur maximum de p.(1-p) soit 0,25 correspondant à p = 0,5. Si l’on veut une approche plus fine qui minimise l’erreur faite sur l’évaluation de la taille, on prend la valeur moyenne soit 0,175 qui correspond à p = 0,226.
Exemple : Calculer la taille d’un échantillon indépendant pour avoir une marge d’erreur de 5 % avec un taux de confiance de 95 % sur une population dont on ne connait pas la proportion.
Le taux de confiance de 95 % nous donne un coefficient de marge t = 1,96.
Prenons un majorant de la taille en prenant p.(1-p) = 0,25. On peut écrire :
n = (1,96)2 x 0,25 / 0,052 = 384
Utilisation d’abaque
On trouve dans la littérature technique différents types d’abaque qui permettent d’évaluer la taille des échantillons.
Le graphique suivant en donne un exemple :
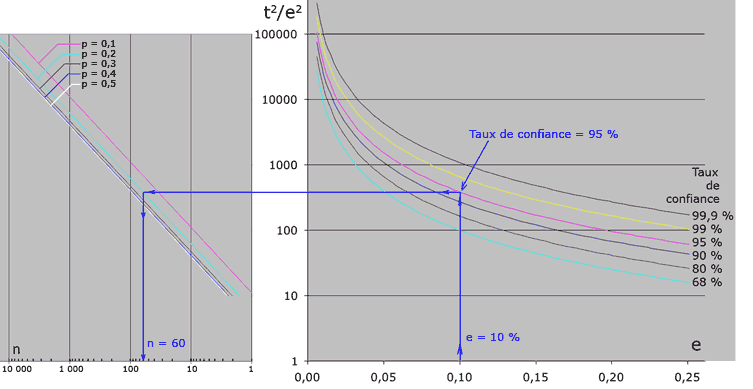
Pour l’utiliser, fixer la valeur de l’erreur admissible (par exemple 0,1), élever une verticale qui croise les courbes correspondant à différents taux de confiance. Au point d’intersection avec la courbe choisie (par exemple taux de confiance = 95 %), on trace une droite horizontale qui croise les courbes correspondant à la proportion dans la population-mère. Au point d’intersection avec la courbe choisie (par exemple p = 0,2, on trace une verticale qui va croiser l’axe des abscisses en un point qui donne la taille de l’échantillon (dans notre exemple 60).
