2 - Estimation à partir d'un échantillon
Introduction
L’estimation consiste à donner la valeur la plus probable d’une grandeur. C’est le problème inverse de l’échantillonnage. On dispose de renseignements sur un ou plusieurs échantillons et on cherche à connaître des informations sur la population-mère.
On peut faire deux types d’estimation :
- L’estimation ponctuelle qui consiste à proposer une valeur pour la grandeur considérée,
- L’estimation par intervalle de confiance qui donne la probabilité que la grandeur soit comprise dans un intervalle donné.
On remarque que la probabilité qu’une estimation ponctuelle soit parfaitement exacte est … nulle, ou enfin voisine de zéro. Il y a donc lieu quand c’est possible, de préférer l’estimation par intervalle de confiance
Estimation ponctuelle
1 – Moyenne
D’une manière générale, on considère que la moyenne d’un échantillon prélevé est la meilleure estimation ponctuelle de la moyenne de la population-mère.
2 – Proportion
de la même façon, on prendra comme estimée ponctuelle de la proportion d’éléments de la population-mère possédant une certaine propriété, la proportion relevée parmi l’échantillon.
3 – Ecart-type
On prend comme meilleur estimée de l’écart-type de la population-mère, la valeur suivante :
![]()
Estimation par intervalle de confiance
La valeur à estimer est une variable aléatoire dont on peut estimer les caractéristiques. La fonction de répartition associée à la loi normale permet d’évaluer l’intervalle à considérer pour obtenir le taux de confiance recherché.
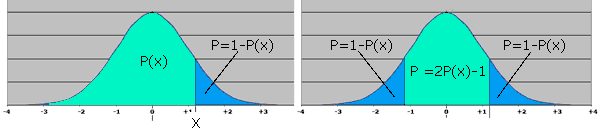
Dans la figure ci-dessus, sur la courbe de gauche, on appelle P(X) la probabilité, lue dans la fonction de répartition, que la variable ait une valeur inférieure à la valeur X. La probabilité que la variable soit supérieure à X est naturellement 1 – P(X).
Sur la courbe de droite, on a évalué la probabilité que la moyenne soit comprise dans l’intervalle [-X :+X]. Cette valeur vaut :
1 – (1 – P(X)) – (1 – P(X)) = 2. P(X) – 1
En inversant la formule, on calcule la valeur qu’il faut lire dans la table de la fonction de répartition pour que la probabilité que la variable soit dans la plage [-X :+X].
P(plage) = 2 x P(table) – 1
d’où
P(table) = (P(plage) + 1) / 2
Par exemple, si l’on souhaite un taux de confiance de 95 %, la valeur à lire dans la table est :
(0,95 + 1)/2 = 0,975 ce qui correspond à la plage [-1,96 ;+1,96]
La courbe suivante donne la variation de l’intervalle à considérer en fonction du taux de confiance requis :
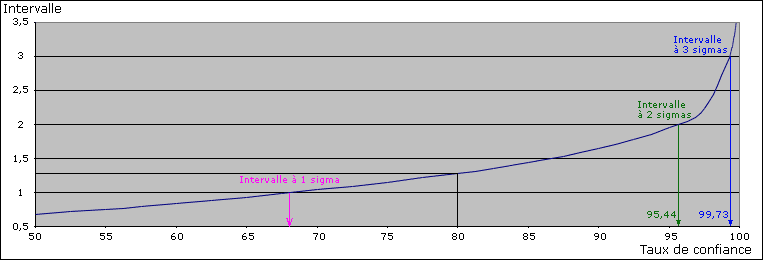
L’estimation consistera à se donner un taux de confiance, à lire sur la courbe précédente l’intervalle normé à considérer. Il suffira de multiplier ce chiffre par l’écart-type de la distribution pour obtenir l’intervalle à prendre en compte.
1 – Moyenne
1 – Evaluation de l’écart-type de la moyenne à estimer
Dans le cas d’un échantillonnage indépendant (non exhaustif), on obtient l’écart-type par la formule suivant :
![]()
Dans la cas d’un échantillonnage exhaustif, c’est la formule suivante qui s’applique :
![]()
2 – Evaluation de l’intervalle à considérer
On se donne alors un taux de confiance qui par lecture dans la courbe précédente nous donne un coefficient t. On obtient alors l’intervalle à prendre en compte :
![]()
Exemple : Soit un échantillon de 100 personnes dont les tailles ont donné une moyenne de 1m75 et dont l’écart-type des tailles est égal à 0m13. Dans quelle plage de taille doit-on considérer cette moyenne pour avoir un taux de confiance de 80 % ?
La courbe donnée plus haut nous indique, pour un taux de confiance de 80 %, un intervalle de : 1,3.
On calcule maintenant l’écart-type de la moyenne dans le cas d’un échantillon indépendant :
0,13 m / 1OO1/2 = 0,013 m
L’intervalle à prendre en compte est dont le suivant :
[1,75 – 1,3 x 0,013 ; 1,75 + 1,3 x 0,013]
soit
[1,7331 m ; 1,7669 m]
2 – Proportion
Il s’agit, à partir de l’échantillon, d’estimer la proportion d’éléments de la population qui ont une propriété donnée.
Estimation ponctuelle
Comme pour la moyenne, on prendra pour valeur estimée d’une proportion dans la population-mère, la proportion mesurée dans l’échantillon. Ce n’est évidemment qu’une valeur approchée sur laquelle on ne peut avoir aucun taux de confiance connu.
Estimation par intervalle de confiance
On suit le même cheminement que pour la moyenne :
1 – Evaluation de l’écart-type de la proportion à estimer
Dans le cas d’un échantillonnage indépendant (non exhaustif), on obtient l’écart-type par la formule suivant :
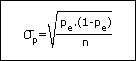
Dans la cas d’un échantillonnage exhaustif, c’est la formule suivante qui s’applique :
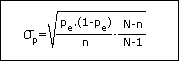
2 – Evaluation de l’intervalle à considérer
On se donne alors un taux de confiance qui par lecture dans la courbe précédente nous donne un coefficient t. On obtient alors l’intervalle à prendre en compte :
![]()
Exemple : Dans le même échantillon que précédemment, on a évalué que 10 % des personnes dépassaient 1m80. Quelle est la proportion estimée pour la population-mère avec un taux de confiance de 95 % ?
La courbe donnée plus haut nous indique, pour un taux de confiance de 95 %, un intervalle de : 1,96.
On calcule maintenant l’écart-type de la moyenne dans le cas d’un échantillon indépendant :
(0,1 x 0,9 / 100)1/2 = 0,00091/2 = 0,03
L’intervalle à prendre en compte est dont le suivant :
[0,1 – 1,96 x 0,03 ; 0,1 + 1,96 x 0,03]
soit
[0,0412 ; 0,1588]
La proportion dans la population-mère est donc comprise entre 4 et 16 %.
