4 - Méthode des moindres carrés

Vous êtes ici: Home » Statistiques » Ajustement statistique » 4 – Méthode des moindres carrés

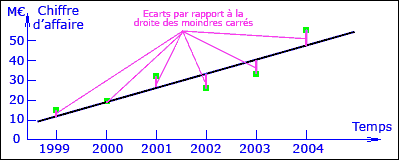
La méthode des moindres carrés consiste à trouver la droite qui minimise la somme des carrés des distances entre chaque point et la droite.

Cette méthode est illustrée par le schéma suivant :

Si la droite cherchée a comme équation y = ax+b, on démontre que les coefficients qui minimisent la somme des carrés des distances sont les suivants :

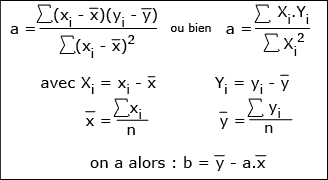
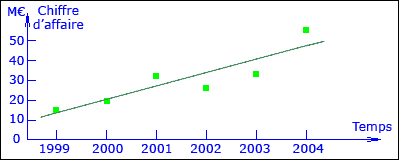
En reprenant l’évolution du chiffre d’affaire traité précédemment on obtient les résultats suivants :

Ce qui donne le tracé de la droite des moindres carrés correspondante :

Vous trouverez sur ce site un graphique interactif illustrant la méthode des moindres carrés.

Généralisation à d’autres courbes d’ajustement

Lorsque l’on doit traiter des phénomènes non linéaires, on peut utiliser à la place de la droite des courbes non linéaires telles que les fonctions exponentielles ou les fonctions mettant en jeu des puissances.

Ajustement exponentiel

Lorsque l’on constate que l’une des variables observées varie de façon géométrique, on ajuste les données par une fonction exponentielle de la forme y = b.a^x. On se ramène alors à un ajustement linéaire par le biais d’un changement de variable logarithmique :

Log y = Log (b.a^x) = Log b + x.Log a.

On peut alors utiliser les formules de l’ajustement linéaire présentées précédemment.

Ajustement par une fonction puissance

Si les deux variables présentent des variations géométriques, on ajuste les données par une fonction puissance de la forme : y = b.x^a

On ramène alors la fonction à un ajustement linéaire par un changement de variable logarithmique :

Log y = Log (b.x^a) = Log b + a.Log x.

On peut alors utiliser les formules précédentes de l’ajustement linéaire.