3 - Caractéristiques de dispersion des séries statistiques
2 – Caractéristiques de dispersion
Intervalle de variation
L’intervalle de variation appelé aussi « étendue » est la différence entre la valeur la plus élevée et la plus faible de la variable statistique. Par définition, la moyenne arithmétique simple se situe au milieu de l’intervalle de variation.
Dans notre exemple, cette valeur vaut : 2,15 m – 1,30 m = 0,85 m.
On peut ainsi caractériser des séries statistiques en terme de plus ou moins grande étendue de variation. Néanmoins, il s’agit d’une grandeur beaucoup moins significative que les caractéristiques qui expriment la dispersion des valeurs par rapport à la valeur moyenne. Cette dispersion fait l’objet de l’écart moyen et de l’écart type.
Ecart moyen
Pour chacune des valeurs, on évalue l’écart par rapport à la valeur moyenne. On considère la valeur absolue des écarts car on ne souhaite pas différentier les valeurs inférieures des valeurs supérieures à la moyenne.
L’écart moyen est la moyenne des valeurs absolues des écarts de l’ensemble des valeurs par rapport à la moyenne (voir schéma ci-dessous).
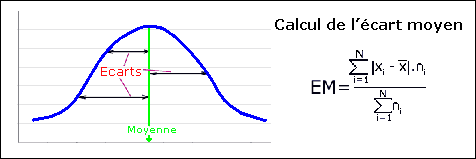
On peut évaluer l’écart moyen de la taille des français avec un résultat de 14,63 cm :
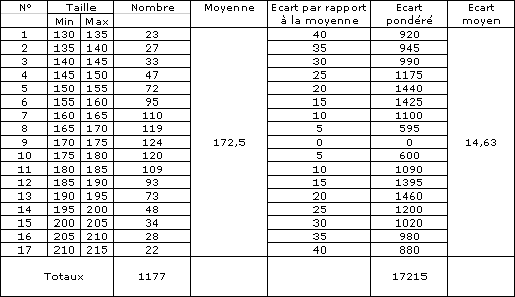
Exemple de calcul d’écart moyen
Une seconde méthode permet de caractériser l’écart de dispersion. Au lieu d’utiliser des valeurs absolues, on procède à l’élévation au carré de chaque écart individuel ce qui permet de rendre positifs tous les écarts. La moyenne de ces écarts sera la variance dont la racine carré donnera l’écart-type.
Variance et écart -type
La variance d’une série statistique est donc la moyenne arithmétique des carrés des écarts des valeurs par rapport à la valeur moyenne. Physiquement, la variance correspond au « taux de variation » de la variable étudiée. L’utilisation du carré des écarts permet d’annuler la compensation due aux sugnes des écarts. L’écart-type est égal à la racine carré de la variance. Il s’exprime dans l’unité de la grandeur qu’il caractérise.
La variance et l’écart-type sont donnés par les formules suivantes :
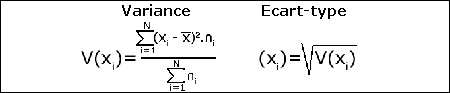
Le tableau suivant applique à l’exemple précédent le calcul de la variance et de l’écart-type :
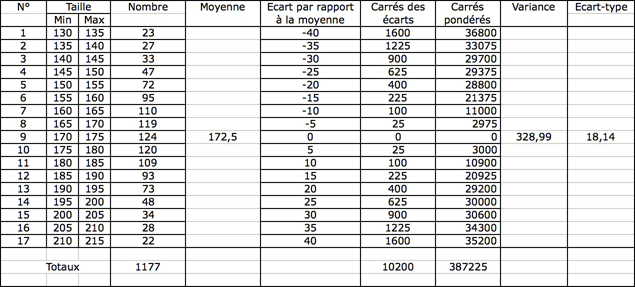
L’écart-type caractérise la dispersion de la série statistique autour de la valeur moyenne. Plus l’écart-type est élevé plus la dispersion est forte.
Dans la pratique l’écart-type sous-estime légèrement l’écart des données par rapport à la moyenne notamment pour les tailles de population ou d’échantillon faible. On a un écart-type et une variance dits « biaisés ». On peut corriger ce biais en multipliant l’écart-type biaisé par la formule suivante :
![]()
Lorsque l’on veut comparer la dispersion de deux séries statistiques, il faut prendre garde à leur valeurs moyennes respectives. On pourra comparer leurs dispersions en « normant » leurs écarts-types par rapport à leurs moyennes en calculant un coefficient de variation égal à l’écart-type divisé par la moyenne.
